Reactive Navigation

We address purely reactive methods that take into account the 3D robot shape, its nonholonomic constraints and different path models.
Generally, obstacle avoidance (OA) methods consider only straight lines or circular arcs to drive the robot towards its target, assuming circular or simple robot shapes and neglecting any kinematic constraint. Transformational approaches exist that extend the applicability of those OA methods to any-shape, nonholonomic robots by means of a space transformation based on a parametrization of circular arcs. We have proven that a wider number of path models, apart from circular arcs, can improve the navigation performance since new feasible movements can be detected and commanded to the robot. We model this variety of path models using the Parameterized Trajectory Generators (PTGs).
Initially, we addressed the problem of reactively driving a kinematically-constrained, any-shape mobile robot in a planar scenario. This problem requires finding movements that approach the target location while avoiding obstacles and fulfilling the robot kinematic restrictions. Our main contribution is related to the process of detecting free-space around the robot, which is the basis for a reactive navigator to decide the best instantaneous motor command.
For this task, we propose a PTG-based reactive navigator that reduces the dimensionality of the Configuration Space (C-Space) from 3D (x, y, φ) to 2D, incorporating in the transformation the geometrical and kinematical constraints of the robot. The robot thus becomes a free-flying point over this 2D manifold embedded in C-Space and the collision avoidance problem is easier and faster to solve.
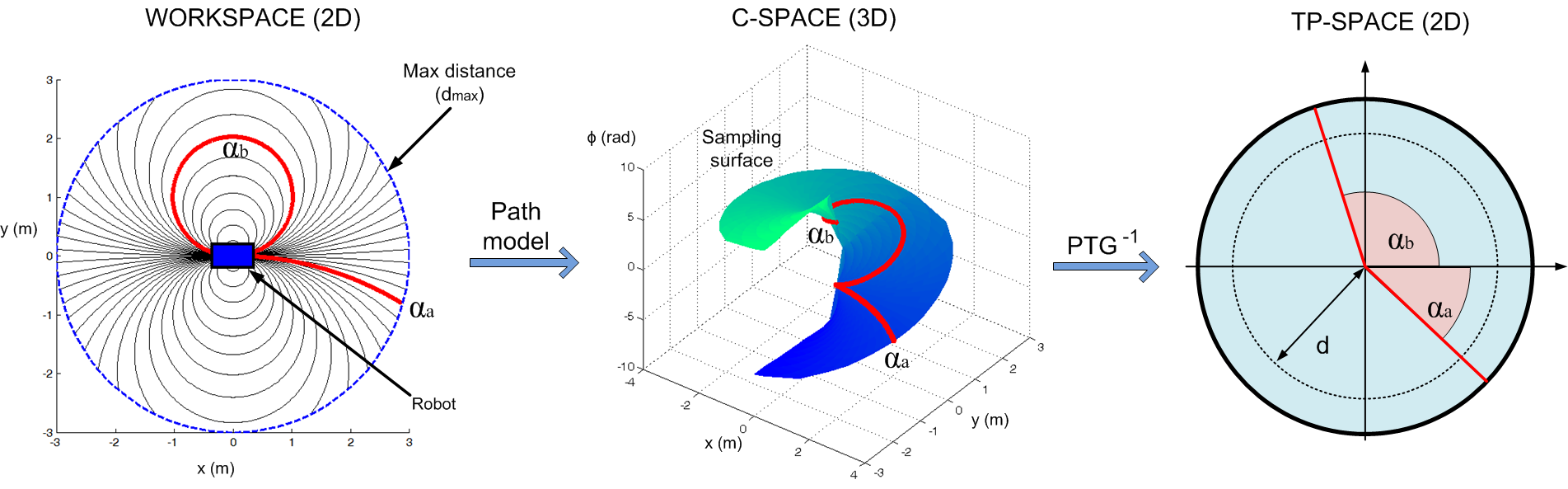
This dimensional reduction is accomplished by restricting the robot motion to one of a set of parametric path models which are compliant with the robot kinematics. The user can define and utilize as many path models as they wish, overcoming the limitation of moving along circular arcs. To choose the best among all the possible motions, we define an objective function that trades off several navigational criteria such (as?) the collision-free distance, the expected deviation from? the target, the difference between the new (tentative) and the previous motion commands (to soften the robot motion), etc.
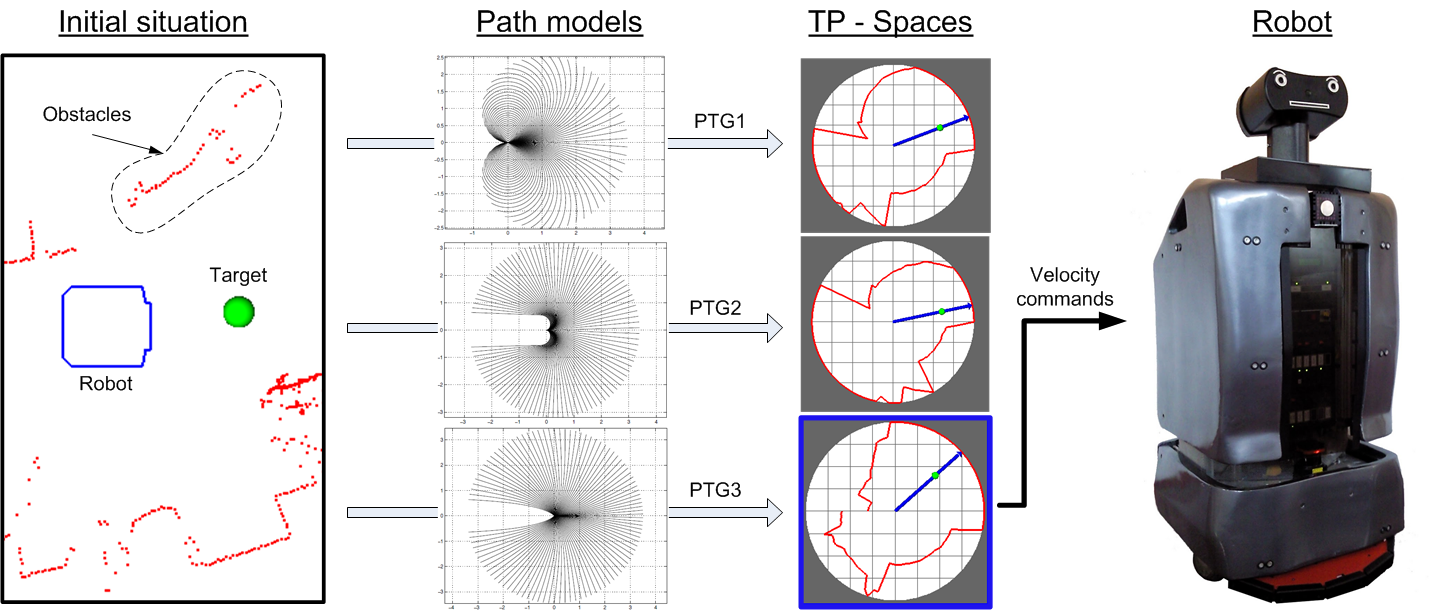
Our approach was tested with two sets of experiments. In the first one, the PTG-based obstacle avoidance method is compared against the more common usage of only one circular path model (with the robot Sancho). The second set was carried out with the robotic wheelchair SENA, and demonstrated safe navigation in a crowded and dynamic area (the entrance of our building at the University of Malaga), with dozens of students walking amid the robot path.
The code is available online within the MRPT: Reactive Navigation App
Traditionally, due to the lack of affordable 3D sensors and the limited computational resources available, reactive navigators have relied on two strong assumptions:
- The world is considered two-dimensional. Since robots usually move on a flat surface, the third dimension (height) is ignored.
- The robot shape is simplified by a polygon or a circle projected onto the 2D world.
These two simplifications force the reactive algorithm to adopt the worst-case scenario, that is, to work with the most restrictive section of the robot and the nearest obstacle detected in each direction. This limitation can complicate or even impede many robotic platforms from carrying their tasks out. However, with the recent emergence of 3D range cameras and the current computational resources on board of robots, these assumptions are no longer justified.

In order to overcome this limitation, we propose a reactive navigator that regards both the 3D shape of the robot and the 3D geometry of the environment. Within this approach, which represents a 3D (or actually 2.5D) generalization of the PTG-based reactive navigator, the robot volume is now modeled by a number of consecutive prisms in height and the detected obstacles are sorted in corresponding height bands. Therefore, as an initial step, we decompose the 3D reactive navigator into N 2D navigators, being N the number of height sections that are used to model the robot geometry. Afterwards, these 2D navigators, which describe the navigability of each robot section in the 3D environment, are consistently and efficiently merged to yield an overall solution.
This work has been extensively tested in varied and challenging scenarios for more than 2 years. Three different robotic platforms were used to test it and are currently working with it to perform higher level tasks. A large amount of experiments were carried out to demonstrate its robustness and its advantages respect to the 2D approach.
The code is available online within the MRPT: 3D Reactive Navigation App




