Localization & Mapping

One of the most fundamental problems in mobile robotics is enabling a robot to localize itself in a previously unknown environment. In the literature this problem is called Simultaneous Localization And Mapping (SLAM), and has witnessed a very intense activity in the robotics community in the last decade.

HMT-SLAM stands for Hybrid Metrical-Topological SLAM. It is a complete, consistent bayesian formulation of the SLAM (Simultaneous Localization and Mapping) problem that copes both with metrical and topological maps. Up to the first published paper of HMT-SLAM, all the intents to include topological information into classical metrical SLAM dealt with topologies as a separate component from metrics, and therefore use different techniques for processing both of them. In HMT-SLAM, however, both parts are dealt with in a unified probabilistic framework, which facilitates the integration of low-level, subsymbolic (metrical) algorithms with high-level, symbolic (topological) reasoning.

Overview

Like most successful works on SLAM, we use Bayesian filtering to provide a probabilistic estimation which can cope with uncertainty in the measurements, the robot pose, and the map. Our approach is based on the reconstruction of the robot path in a hybrid discrete-continuous state space, which naturally combines metric and topological maps. There are two fundamental characteristics of HMT-SLAM that set it apart from previous works:

• The use of a unified Bayesian inference approach both for the metrical and the topological parts of the problem.
• The analytical formulation of belief distributions over hybrid maps, which allows us to maintain the partial uncertainty in large spaces more accurately and efficiently than previous works.

This method ideas has been validated by promising experimental results in large environments (up to ~30.000 m², a 2Km robot path) with multiple tested loops, which could hardly be managed appropriately by other approaches.

We introduce the concept of the hybrid metric-topological (HMT) path, which comprises the sequence of areas the robot has traversed (topological part) and its pose within each of them (metric part). Then, by considering the posterior belief distribution of the whole HMT path we can obtain he probability distribution over all the potential topological structures of the environment, an issue not addressed before simultaneously to the estimation of the metric poses between, and within, the areas. The resulting probabilistic map, called HMT map, represents the topology of the environment ith graphs whose nodes (areas) are annotated with metric sub-maps and whose arcs (connections between areas) are annotated with the coordinate transformations between the corresponding areas.This model is illustrated in the following figure:

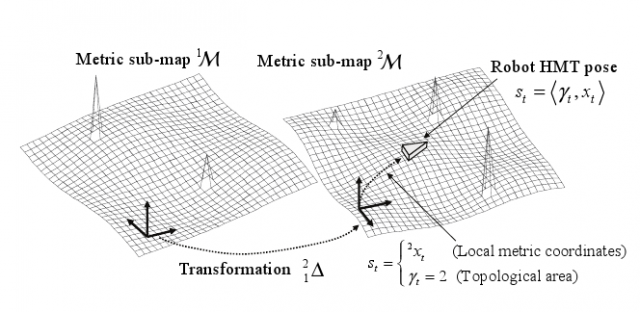
By conditioning the belief distribution of the map to the knowledge of the HMT path, we can represent these relative coordinate transformations in closed form, avoiding by design some problems that appear in global mapping with particle filters. The avoidance of absolute coordinates has been repeatedly proposed in the literature due to the difficulty of appropriately representing the uncertainty of poses far away from a global coordinate origin. Our approach,  HMT-SLAM, supports metric sub-maps of either landmarks or occupancy grid-maps. In the context of occupancy grid mapping, it naturally provides a correction of the robot path after closing large loops without rebuilding any global metric map, which has been pointed out sometimes as a weakness of grid-based, large-scale mapping.

Results

The next video shows one of the successfully built maps constructed by our approach. In this case, the dataset consists of a path of ~2Km gathered by our robotic wheelchair SENA while guided through the building of ETSI Telecomunicación in Málaga. Notice the high number of loop closures, some of them nested. Other state-of-the-art approaches would hardly manage successfully and with a similar efficiency the building of such maps.