Dr. Jesús Briales – MAPIR Research Group

Former member

I am Jesus Briales, a researcher in the Machine Perception and Intelligent Robotics group (MAPIR) at the University of Malaga (Spain). My research interests lie in the area of computer vision and include:

Visual odometry, SLAM, Structure from Motion.
Sensor fusion.
Convex relaxations, Global optimization, Riemannian manifolds.

I have been doing research since October 2013 when I joined the MAPIR group as a Research Assistant. I received my Bacherlor’s and Master’s degree in Industrial Engineering (a general engineering which covers mechanics, electricity, electronic, computer science, etc.) from the University of Malaga in 2014. Since October 2015 I hold a FPU grant from the Spanish government to pursue a PhD in Computer Vision under the supervision of Prof. Javier Gonzalez-Jimenez. From March to July 2017 I was a guest researcher at the Computer Vision group of Chalmers University (Sweden), under the supervision of Prof. Fredrik Kahl. From January to July 2018 I was an intern at Oculus Research, under the supervision of Hauke Strasdat.

Contents

Research (from most recent to oldest)
Publications
Contact

Research (from most recent to oldest)

Global optimality in registration problems:

Registration is a fundamental problem in Computer Vision, where we seek in general to align several models/measurements. Models generated by state-of-the-art methods consist of multiple kind of features (planes, lines, points), and no closed-form solution exists for the corresponding multi-modal registration problem.

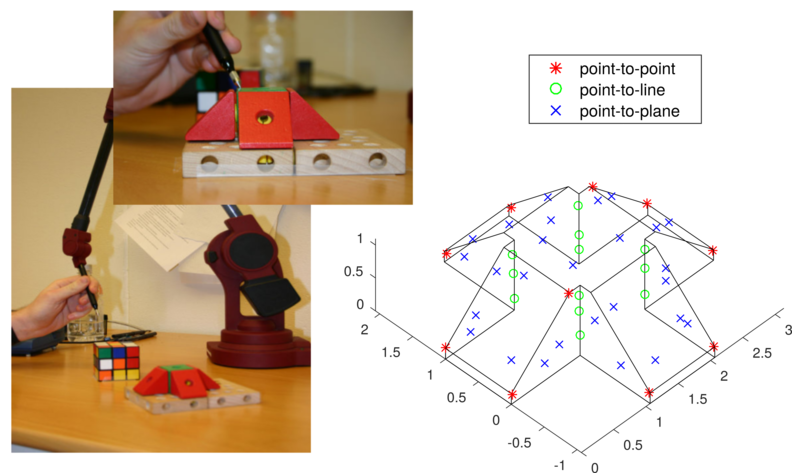
Rigid registration: For rigid registration problems, where we seek an unknown pose, Lagrangian duality can be used to find the globally optimal transformation aligning a general geometric model and multiple measurements. In “Convex Global 3D Registration with Lagrangian Duality” (CVPR17) we present a novel relaxation strategy (based on Lagrangian duality) that (empirically) returned the global solution for the original registration problem in all evaluated cases for a wide variety of problems. One of the key aspects in this approach was the exploitation of redundant constraints in the context of rotations, an overlooked aspect that turns essential for effectively relaxing rotation constraints.

Global optimality of solutions in SLAM:

State-of-the-art approaches for SLAM take a graph-based approach that seeks the best model from the consensus of many available measurements from different devices. This problem becomes hard due to both the inherent non-linearities in the problem as well as the scalability issues with map size. As a result, we end up with a high-dimensional non-linear problem that is addressed through local iterative optimization techniques.

Pose Graph Optimization (PGO): For the case of PGO problems, Lagrangian duality makes it possible to characterize the global optimal solution of PGO when strong duality is fulfilled (and this happens very often). In “Fast Global Optimality Verification in 3D SLAM” (IROS16) we proposed a novel formulation of the SLAM problem and exploited it to verify optimality much faster than the contemporary state-of-the-art method. Then, in “Initialization of 3D Pose Graph Optimization using Lagrangian duality” (ICRA17) we used this same formulation to recover the globally optimal solution to PGO if there is strong duality, or a remarkably good initialization otherwise. Our last work “Cartan-Sync: Fast and Global SE(d)-Synchronization” (under review in RAL) provides a fast and scalable way to solve the underlying dual problem, so that solving PGO globally becomes affordable in real applications.

Line-based monocular odometry:

Most state-of-the-art odometry and SLAM pipelines use point features only, so their behavior may degrade in low-textured scenarios. Human-made scenarios are structured and provide a lot of information as line segments.

The introduction of line segments in traditional odometry pipelines rendered previous proposals notably slow. In “PL-SVO: Semi-Direct Monocular Visual Odometry by Combining Points and Line Segments” (IROS16) we propose an extension of a successful semi-direct approach, SVO, that exploits both point and line segment features. It works in a wider variety of scenarios and, very important, it keeps real-time performance.

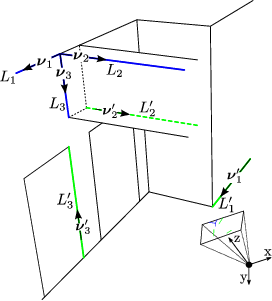
In “A minimal closed-form solution for the Perspective Three orthogonal Angles (P3oA) problem. Application to visual odometry” (JMIV16) we provide a simple closed-form solution to the Perspective Three orthogonal Angles (P3oA) problem: given the projection of three orthogonal lines in a calibrated camera, find their 3D directions. Upon this solution, an algorithm for the estimation of the camera relative rotation between two frames is proposed.

Extrinsic sensor calibration: Laser and camera

Robots are often equipped with 2D laser-rangefinders (LRFs) and cameras since they complement well to each other. In order to correctly combine measurements from both sensors a precise estimation of their relative pose (or extrinsic calibration) is required.

In “Extrinsic Calibration of a 2D Laser-Rangefinder and a Camera based on Scene Corners” (ICRA15) we proposed a novel approach for this calibration problem that exploits the geometric information gathered from multiple observations of a Manhattan-like structured environment, circumventing the necessity of an on-purpose calibration pattern. Then, in “A minimal solution for the Calibration of a 2D Laser-Rangefinder and a Camera based on Scene Corners” (IROS15) we contributed a closed-form solution for the problem above when using the minimal amount of data, which comes down to barely one single observation of an orthogonal trihedron.